Jako člen také získáte neomezený přístup k více než 88,000 88,000 lekcím matematiky, angličtiny, přírodních věd, historie a dalších. Navíc získáte cvičné testy, kvízy a personalizované koučování, které vám pomohou uspět. Získejte neomezený přístup k více než XNUMX XNUMX lekcím. Zkuste to bez rizika
Nastavení trvá jen několik minut a můžete jej kdykoli zrušit. Zabere to jen pár minut. Kdykoli zrušit.
Již zaregistrované? Pro přístup se přihlaste zde
Co říkají učitelé o Study.com
Vyzkoušejte to bez rizika po dobu 30 dnů Již jste zaregistrováni? Pro přístup se přihlaste zde
- 00:04 Identifikace pozitivních a…
- 02:36 Identifikace pozitivních a…
Jak identifikovat pozitivní a negativní zrychlení
Krok 1: Zapište si časový interval podle místa, kde se počítá zrychlení.
Krok 2: Zapište počáteční a konečné hodnoty rychlosti pro referenční časový interval.
Krok 3: Vypočítejte změnu rychlosti. Kladné nebo záporné znaky změny rychlosti určí, zda je zrychlení kladné nebo záporné.
Co je zrychlení a kdy je pozitivní nebo negativní?
Rychlost: Je to referenční hodnota pro kvantifikaci toho, jak rychle a jakým směrem se objekt pohybuje. Rychlost (V) je vektorová veličina, která udává velikost a směr. V této lekci uvažujeme o pohybu po přímce, proto jsou možné dva směry: pozitivní nebo negativní.
Změna rychlosti: Jeho hodnotu lze vypočítat odečtením počáteční neboli referenční rychlosti (Vi) od konečné neboli proudové rychlosti (Vf).
Změna rychlosti = trojúhelník V = Vf-Vi
Jednotky rychlosti: Jednotky pro měření rychlosti jsou definovány rozdělením mezi jednotkou používanou k měření posunutí a jednotkou používanou k měření času. Nejpoužívanějšími jednotkami rychlosti jsou kilometry za hodinu (km/h), míle za hodinu (Mph) a metry za sekundu (m/s). Jako posledně jmenovaná jednotka navržená Mezinárodní soustavou jednotek (SI).
Akcelerace: Je to vektorová veličina aplikovaná k měření změn (směru a velikosti) rychlosti. Zrychlení udává změny v rychlosti pohybu objektu a změny směru.
Vzorec zrychlení: Průměrná hodnota pro zrychlení (a) se vypočítá jako změna rychlosti dělená časem (t), který trvalo, než k této změně došlo.
Protože hodnota času bude vždy kladná, změna rychlosti určuje, zda je zrychlení kladné nebo záporné. Pokud je změna rychlosti nulová (množství zůstává stejné), pak bude zrychlení také nulové.
Jednotky zrychlení: Zrychlení je dáno jednotkou složenou z dělení mezi jednotkou rychlosti a časovou jednotkou. Nejčastěji je jednotka pro zrychlení dána jednotkou navrženou SI, což je rm m/s^2 (metry za sekundu, za sekundu). Nicméně různé jednotky jako rm Km/h^2 a lze použít rm frac.
Pokusme se tyto kroky a koncepty aplikovat na následující dva příklady!
Příklady toho, jak identifikovat pozitivní a negativní zrychlení
Příklad 1
Níže uvedená tabulka ukazuje 4 hodnoty rychlosti a jim odpovídající časové značky. Určete, zda bylo průměrné zrychlení celého pohybu kladné, záporné nebo nulové.
| Rychlost | Čas |
|---|---|
| 4 m / s | 2 s |
| 1 m / s | 4 s |
| -2 m/s | 6 s |
| -8 m/s | 10 s |
Krok 1: Zapište si časový interval podle místa, kde se počítá zrychlení.
Vzhledem k tomu, že problém se ptá na průměrné zrychlení aplikované na celý pohyb, budou uvažovány známky prvního a čtvrtého času, respektive 2 s a 10 s. V tomto intervalu 8 s bude analyzováno průměrné zrychlení.
Krok 2: Zapište počáteční a konečné hodnoty rychlosti pro referenční časový interval.
Po 2 s máme počáteční rychlost 4 m/s (Vi = 4 m/s) a po 10 s máme konečnou rychlost -8 m/s (Vf = -8 m/s)
Krok 3: Vypočítejte změnu rychlosti. Kladné nebo záporné znaky změny rychlosti určí, zda je zrychlení kladné nebo záporné.
Použití hodnot z předchozích kroků k nalezení změny rychlosti má za následek:
trojúhelník V = Vf-Vi trojúhelník V = rm (-8 m/s)-4 m/s = -12 m/s
Protože zrychlení je dáno trojúhelník V děleno vždy kladnou hodnotou trojúhelník t , pak bude zrychlení pro tento příklad záporné.
Příklad 2
Předmět, zpočátku v klidu, se pohybuje po dobu 20 sekund, dokud nedosáhne rychlosti 50 m/s. Určete, zda bylo jeho zrychlení kladné, záporné nebo nulové.
Krok 1: Zapište si časový interval podle místa, kde se počítá zrychlení.
Časový interval je Delta t=20 textových s
Krok 2: Zapište počáteční a konečné hodnoty rychlosti pro referenční časový interval.
Protože objekt zahájil pohyb v klidu, jeho počáteční rychlost v čase nula bude také nulová. Uplynulý čas byl 20 sekund, kdy jeho rychlost dosáhla 50 m/s.
Krok 3: Vypočítejte změnu rychlosti. Kladné nebo záporné znaky změny rychlosti určí, zda je zrychlení kladné nebo záporné.
trojúhelník V = Vf-Vi trojúhelník V = rm 50 m/s-0 = 50 m/s
Tato hodnota znamená, že změna rychlosti je kladná, a proto je zrychlení kladné.
- Julio Gea-Banacloche
- University of Arkansas prostřednictvím knihoven University of Arkansas
Průměrné a okamžité zrychlení
Stejně jako jsme v předchozí kapitole definovali průměrnou rychlost, pomocí konceptu posunu (nebo změny polohy) za časový interval (Delta t) definujeme průměrné zrychlení v průběhu času (Delta t) pomocí změny rychlosti: [ a_=frac=frac-v_>-t_> label .] Zde jsou (v_i) a (v_f) počáteční a konečné rychlosti, tj. , rychlosti na začátku a na konci časového intervalu (Delta t). Stejně jako v případě průměrné rychlosti je však průměrné zrychlení konceptem poněkud omezené užitečnosti, takže bychom mohli rovnou přejít k definici okamžité zrychlení (nebo jen „zrychlení“, bez modifikátorů), prostřednictvím stejného druhu omezovacího procesu, kterým jsme definovali okamžitou rychlost: [ a=lim _ frac label .] Vše, co jsme si řekli v předchozí kapitole o vztahu mezi rychlostí a pozici lze nyní říci o vztahu mezi zrychlením a rychlostí. Například (pokud znáte počet), zrychlení jako funkce času je derivací rychlosti jako funkce času, což z něj dělá druhou derivaci polohové funkce: [ a=frac=frac x>> label ] (a pokud ano ne ještě znáte kalkul, nebojte se horních indexů „2“ na tom posledním výrazu! Je to jen zvláštní zápis, který se jednou naučíte.) Podobně můžeme „odečíst“ okamžité zrychlení z rychlost graf versus čas, pohledem na sklon přímky tečné ke křivce v libovolném bodě. Pokud však to, co je nám dáno, je a pozice oproti časovému grafu je souvislost se zrychlením více nepřímá. Obrázek (PageIndex) vám poskytne takový příklad. Podívejte se, zda dokážete uhodnout, ve kterých bodech podél této křivky je zrychlení kladné, záporné nebo nulové. Způsob, jak to udělat „od nuly“, je pokusit se nejprve zjistit, co dělá rychlost, a z toho odvodit zrychlení. Zde je návod, jak by to šlo: Počínaje (t) = 0 a při sledování sklonu křivky (x)-vs-(t) můžeme vidět, že rychlost začíná na nule nebo blízko nule a neustále se zvyšuje. na chvíli, dokud (t) není o něco více než 2 s (řekněme (t) = 2.2 s pro definitivnost). To by odpovídalo periodě kladného zrychlení, protože (Delta v) by bylo kladné pro každé (Delta t) v tomto rozsahu.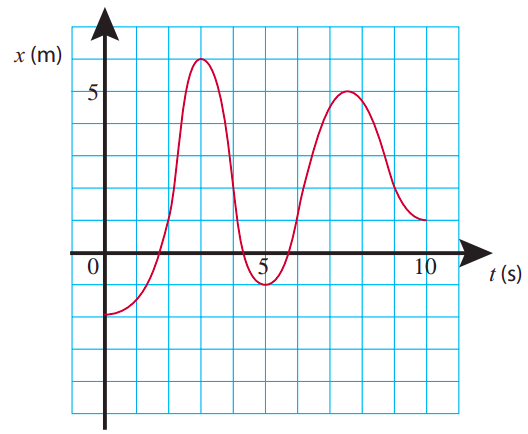 
Mezi (t) = 2.2 s a (t) = 2.5 s, když se objekt pohybuje z (x) = 2 m do (x) = 4 m, se nezdá, že by se rychlost příliš měnila a odpovídajícím způsobem by bylo zrychlení. nula nebo blízko nuly. Poté, kolem (t) = 2.5 s, začne rychlost znatelně klesat a stane se (okamžitě) nulovou při (t) =3 s ((x) = 6 m). To by odpovídalo zápornému zrychlení. Všimněte si však, že rychlost poté dále klesá a stává se stále zápornější až do doby kolem (t) = 4 s. To také odpovídá zápornému zrychlení: i když objekt zrychluje, zrychluje se v záporném směru, takže (Delta v), a tedy (a), je záporné pro každý časový interval. Došli jsme k závěru, že (a < 0) pro všechny časy mezi (t) = 2.5 sa (t) = 4 s. Dále, když se podíváme za (t) = 4 s, stane se ještě něco zajímavého: objekt se stále pohybuje v záporném směru (záporná rychlost), ale nyní se zpomaluje. Matematicky to odpovídá a pozitivní zrychlení, protože algebraická hodnota rychlosti ve skutečnosti roste (číslo jako −3 je větší než číslo jako −5). Jiný způsob, jak o tom přemýšlet, je, že pokud máme méně a méně negativních věcí, náš celkový trend je pozitivní. Takže zrychlení je kladné po celou dobu od (t) = 4 s až (t) = 5 s (kde je rychlost okamžitě nulová, když se směr pohybu objektu obrátí), a dále, dokud nebude přibližně (t) = 6 s, protože mezi (t) = 5 sa (t) = 6 s je rychlost kladná a roste. Pravděpodobně můžete sami nyní přijít na to, co se stane po (t) = 6 s, uvažujte stejně jako já výše, ale možná jste si také všimli vzoru, který tento druh analýzy značně usnadňuje. Zrychlení (jak už možná pochopili ti, kdo mají znalosti kalkulu), které je úměrné druhé derivaci funkce (x(t)) vzhledem k (t), přímo souvisí s zakřivení grafu (x)-vs-(t). Jak ukazuje obrázek (PageIndex) níže, pokud je graf konkávní (někdy nazývané „konkávní nahoru“), zrychlení je kladné, zatímco je záporné, kdykoli je graf konvexní (nebo „konkávní směrem dolů“). Je (okamžitě) nula v těch bodech, kde se mění zakřivení (které možná znáte jako inflexní body), stejně jako v průběhu času, kdy je graf (x)-vs-(t) přímka (pohyb s konstantní rychlostí). 
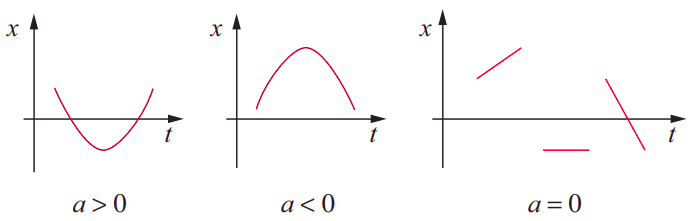Obrázek (PageIndex) ukazuje polohu, rychlost a zrychlení v závislosti na čase pro případ hypotetického pohybu. Pečlivě si jej prostudujte, dokud nebude každý prvek každého grafu dávat smysl vzhledem k ostatním dvěma! Mnoho dalších příkladů toho uvidíte v domácím úkolu a v laboratoři. 
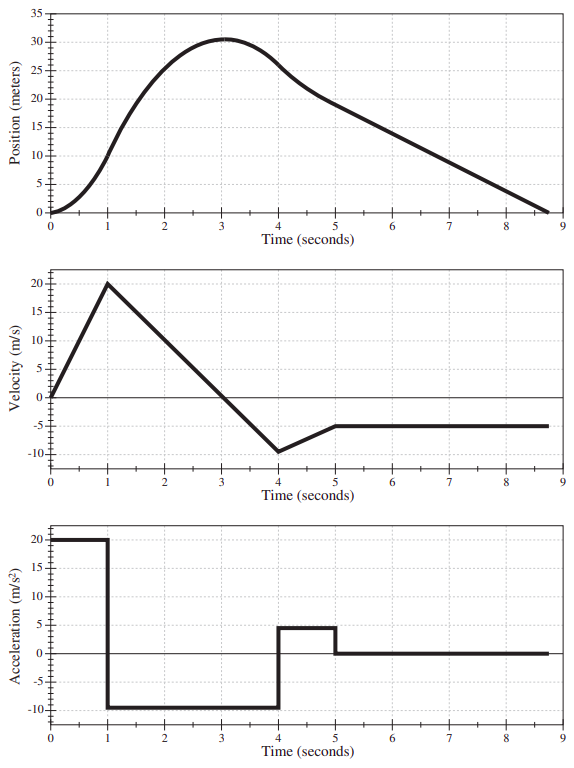Všimněte si, že na všech těchto obrázcích nemá znaménko (x) nebo (v) v daném okamžiku nic společného se znaménkem (a) ve stejnou dobu. Je pravda, že například záporné (a), pokud trvá dostatečně dlouhou dobu, nakonec vyústí v záporné (v) (jak se to děje například na obrázku (PageIndex) v intervalu od (t) = 1 až (t) = 4 s), ale to může trvat dlouho v závislosti na velikosti (a) a počáteční hodnotě (v). Grafická vodítka, která je třeba následovat, jsou: zrychlení je dáno sklonem tečny ke křivce (v)-vs-(t) nebo zakřivením křivky (x)-vs-(t), jako vysvětleno na obrázku (PageIndex); a rychlost je dána sklonem tečny ke křivce (x)-vs-(t). (Poznámka: Abychom si usnadnili interpretaci obrázku (PageIndex), zvolil jsem zrychlení tak, aby bylo „po částech konstantní“, tedy konstantní v prodloužených časových intervalech a nespojitě se měnící hodnota z jednoho intervalu na druhý. To je fyzikálně nereálné: v jakékoli reálné situaci by se očekávalo, že se zrychlení bude více či méně plynule měnit z okamžiku na okamžik. Příklady toho uvidíme později, až se začneme dívat na realistické modely srážek.)
Pohyb S konstantním zrychlením
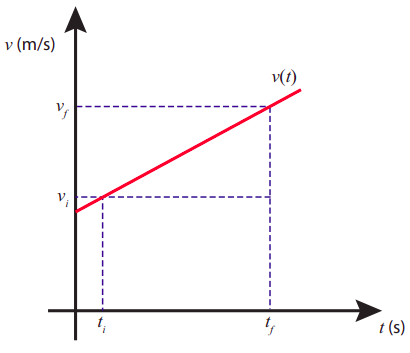
Zvláštním druhem pohybu, který je zároveň relativně jednoduchý a v praxi velmi důležitý, je pohyb s konstantním zrychlením (příklady opět viz obrázek (PageIndex). Pokud je (a) konstantní, znamená to, že se rychlost mění s časem konstantní rychlostí, o pevný počet m/s každou sekundu. (To jsou mimochodem jednotky zrychlení: metry za sekundu za sekundu, neboli m/s 3 .) Změna rychlosti za časový interval (Delta t) je pak dána [ Delta v = štítek Delta t ], který lze také napsat [ v=v_+left(t-t_right) label .] Rovnice (ref) je tvar funkce rychlosti ((v) jako funkce (t)) pro pohyb s konstantním zrychlením. To zase musí být derivace vzhledem k času odpovídající polohové funkce. Pokud znáte jednoduché derivace, můžete ověřit, že vhodný tvar funkce pozice musí být [ x=x_+v_left(t-t_right)+frac aleft(t-t_right)^ label ] nebo pokud jde o intervaly, [ Delta x=v_ Delta t+frac a(Delta t)^ štítek .] Nejčastěji se rovnice (ref) píše s implicitním předpokladem, že počáteční hodnota t je nula: [ x=x_+v_ t+frac a t^ štítek .] Toto je jednodušší, ale ne tak obecné jako rovnice (ref). Vždy se ujistěte, že víte, jaké podmínky platí pro jakoukoli rovnici, kterou se rozhodnete použít! Jak můžete vidět z rovnice (ref), pro intervaly, během kterých je zrychlení konstantní, by měla být křivka závislosti rychlosti na čase přímka. Obrázek (PageIndex) to ilustruje. Rovnice (ref) na druhé straně ukazuje, že pro tytéž intervaly by křivka pozice vs. čas měla být (část a) paraboly, a opět to lze vidět na obrázku (PageIndex) (někdy, pokud zrychlení je malé, zakřivení grafu může být špatně vidět, to se děje na obrázku (PageIndex) pro interval mezi (t) = 2 sa (t) = 3 s). Pozorování, že (v)-vs-(t) je přímka, když je zrychlení konstantní, nám poskytuje jednoduchý způsob, jak odvodit rovnici (ref), v kombinaci s výsledkem (z konce předchozí kapitoly), že posunutí za časový interval (Delta t) se rovná ploše pod křivkou (v)-vs-(t) pro tento časový interval. Skutečně zvažte situaci znázorněnou na obrázku (PageIndex). Celková plocha pod zobrazeným segmentem se rovná ploše obdélníku základny (Delta t) a výšce (v_i), plus plocha trojúhelníku základny (Delta t) a výšce (v_f − v_i). Protože (v_f − v_i = aDelta t), jednoduchá geometrie okamžitě dává rovnici (ref) nebo její ekvivalent (ref). Nakonec zvažte, co se stane, když vyřešíme rovnici (ref) pro (Delta t) a dosadíme výsledek do (ref). Dostaneme [ Delta x=frac +frac label .] Nechat (Delta v = v_f − v_i), trocha algebry vede k [ v_^-v_^=2 a Delta x label .] Toto je praktický malý výsledek, který lze také viděno tak, aby přímo vycházelo z teorémů pracovní energie, které budou představeny v kapitole 7 1 . 1 Ve skutečnosti se rovnice (odkaz) ukazuje být tak užitečná, že ji pravděpodobně budete v tomto semestru používat znovu a znovu a můžete být dokonce v pokušení použít ji pro problémy zahrnující pohyb ve dvou dimenzích. Pokud však opravdu nevíte, co děláte, měli byste odolat pokušení, protože je velmi snadné použít rovnici (ref) nesprávně, když zrychlení a výchylka neleží na stejné přímce. Místo toho byste měli použít vhodnou formu teorému práce-energie.
Akcelerace jako vektor
Zrychlení v různých referenčních rámcích
V kapitole 1 jste viděli, že mezi rychlostmi částice P měřenými ve dvou různých vztažných soustavách A a B platí následující vztah: [ vec_=vec_+vec_ label .] A co zrychlení? Rovnice jako (ref) bude platit pro počáteční a konečnou rychlost a jejich odečtením dostaneme [ Delta vec_=Delta vec_+Delta vec_ label .] Nyní předpokládejme, že se referenční rámec B pohybuje s konstantní rychlost vzhledem k snímku A. V tom případě (vec v_ = vec v_), takže (Delta vec v_ ) = 0, a pak vydělení rovnice (ref) (Delta t) a převzetí limity (Delta t šipka vpravo 0) , dostaneme [ left.vec_=vec_ quad text vec_right) popisek .] Pokud se tedy dva referenční rámce vzájemně vůči sobě pohybují konstantní rychlostí, pozorovatelé v obou snímcích měří stejný zrychlení pro jakýkoli objekt, který mohou oba sledovat. Výsledná rovnice (ref) znamená zejména, že máme-li inerciální soustavu, pak každá soustava pohybující se konstantní rychlostí vůči ní bude také inerciální, protože příslušná měření pozorovatelů budou souhlasit s tím, že rychlost objektu se nemění (jinak řečeno, jeho zrychlení je nulové), když na něj nepůsobí žádné síly. Naopak zrychlený rám bude ne být inerciální soustava, protože rovnice (ref) nebude platit. To je v souladu s příklady, které jsem zmínil v části 2.1 (poskakující rovina, auto při zastavování). Dalším příkladem neinerciálního rámu by bylo auto projíždějící zatáčkou, i když jede konstantní rychlostí, protože, jak jsem právě uvedl výše, jde také o zrychlený systém. To je potvrzeno skutečností, že předměty v takovém voze mají tendenci se pohybovat – vzhledem k autu – směrem k vnější straně zatáčky, i když na ně nepůsobí žádná skutečná síla.
Tato stránka s názvem 2.2: Acceleration je sdílena pod licencí CC BY-SA 4.0 a byla vytvořena, remixována a/nebo kurátorem vytvořena Julio Gea-Banacloche (University of Arkansas Libraries) prostřednictvím zdrojového obsahu, který byl upraven podle stylu a standardů platforma LibreTexts; podrobná historie úprav je k dispozici na vyžádání.
- Byl tento článek užitečný?
- Ano
- Ne
